18. Deutsch 算法#
Deutsch 算法(基于oracle的算法)#
我们应该首先了解 oracle 的概念,可以被认为是一个黑盒子,例如有人设计了一个经典电路,而没有向你解释它是什么,并且你不被允许查看它。
出于实际目的,我们仅指经典计算部分, $\( \boxed{ |x\rangle|0\rangle \rightarrow|x\rangle|f(x)\rangle } \)\( 我们不在乎\)f(x)$是如何构造的。
此外,我们还可以进行以下操作(针对布尔函数) $\( \boxed{ |x\rangle \rightarrow (-1)^{f(x)}|x\rangle } \)\( 我们可以通过以下方式实现(有时称为相位反冲)(在叠加状态中添加额外的辅助量子比特): \)\( U_{\mathrm{CNOT}}|f(x)\rangle(|0\rangle-|1\rangle)=|f(x)\rangle(|0 \oplus f(x)\rangle-|1 \oplus f(x)\rangle)=(-1)^{f(x)}|f(x)\rangle(|0\rangle-|1\rangle) \)\( 换句话说,我们必须应用序列(忽略一些辅助量子比特): \)\( |x\rangle \rightarrow|x\rangle|f(x)\rangle \rightarrow(-1)^{f(x)}|x\rangle|f(x)\rangle \rightarrow(-1)^{f(x)}|x\rangle \)\( Deutsch 算法解决了以下问题:给定一个 oracle 布尔函数\)f(x)$,它将一比特作为输入,一比特作为输出。有两种可能性:constant 或 balanced。
情况 1(constant):\(f(0) = f(1)\)
两种可能,\(f(0)=f(1)=0\) 或 \(f(0)=f(1)=1\)
情况 2(balanced):\(f(0) \ne f(1)\)
两种可能,\(\{f(0)=1,f(1)=0\}\) 或 \(\{f(0)=0,f(1)=1\}\)
传统上,必须对函数进行两次评估。如果你只调用一次oracle,你只能知道 \(f(0)\) 或 \(f(1)\),但不能同时知道两者。而 Deutsch 算法允许我们通过只调用一次oracle来解决问题(确定它是情况 1 还是情况 2)。
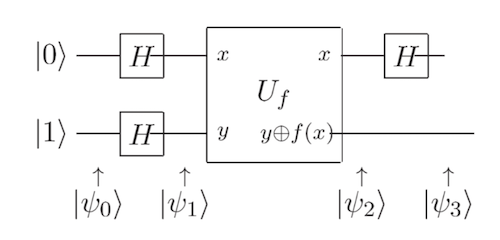
步骤1:
让我们首先创建输入的叠加,即 $\( H|0\rangle = \frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \)$
步骤2:
我们应用oracle: $\( \frac{1}{\sqrt{2}}\left((-1)^{f(0)}|0\rangle+(-1)^{f(1)}|1\rangle\right) \)\( 请注意,如果是情况 1,那么这只是\)|+\rangle\((差一个正负号); 如果是情况 2,那么我们有\)|-\rangle$(差一个正负号)。
步骤3:
最后,我们只需要区分\(|+\rangle\)或\(|-\rangle\)态,可以通过作用 Hadamard 门来实现:\(H|+\rangle=|0\rangle\),\(H|-\rangle=|1\rangle\)
from mindquantum.core.gates import H, X, I, Measure, BARRIER
from mindquantum.core.circuit import Circuit
from mindquantum.simulator import Simulator
import numpy as np
constant = I.on(1, 0)
balanced = X.on(1, 0)
# 使 oracle 随机为 constant 或 balanced 的情况
rnd = np.random.rand()
if rnd < 0.5:
Uf = constant
else:
Uf = balanced
circ = Circuit()
circ += X.on(1)
circ += BARRIER
circ += H.on(0)
circ += H.on(1)
circ += Uf
circ += H.on(0)
circ += Measure().on(0)
print(circ)
sim = Simulator('mqvector', circ.n_qubits)
res = sim.sampling(circ, shots=100)
res
┏━━━┓ ┏━━━┓ ┍━━━━━━┑
q0: ────────┨ H ┠───■───┨ H ┠─┤ M q0 ├───
┗━━━┛ ┃ ┗━━━┛ ┕━━━━━━┙
┏━━━┓ ┏━━━┓ ┏━┻━┓
q1: ──┨╺╋╸┠─┨ H ┠─┨ I ┠──────────────────
┗━━━┛ ┗━━━┛ ┗━━━┛
shots: 100 Keys: q0│0.00 0.2 0.4 0.6 0.8 1.0 ────────┼───────────┴───────────┴───────────┴───────────┴───────────┴ 0│▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓▓ │ {'0': 100}
可以多次运行以上代码,观察不同情况下的测量结果。实践中我们需要引入辅助比特 \(q_1\) 来实现\(|x\rangle|y\rangle\rightarrow |x\rangle|y\oplus f(x)\rangle\),并且可以用控制 \(I\) 门实现 constant 情况,用 \(CNOT\) 门实现 balanced 情况。可以看到,当 oracle 是情况 1(constant)时,测量结果全为 0 ;而情况 2(balanced)时,测量结果全为 1 。
Deutsch-Jozsa 算法#
后来,Jozsa 与 Deutsch 合作,将原始算法扩展到多个量子比特案例。
Deutsch-Jozsa 算法求解的问题如下:
给定一个 n 比特布尔函数的oracle,\(f(x)\rightarrow \{0,1\}\),对于任意\(x \in \{0,1\}^n\)
(promised problem)确定两种情况:constant 或 balanced
constant: 对于所有的\(x\)都有 \(f(x)=0\) 或 \(f(x)=1\)
balanced:(\(f(x)=0\) 的数量)=(\(f(x)=1\) 的数量)
现在这是一个更加人造的问题。
示例:对于两比特情况:
constant: \(f(00)=f(01)=f(10)=f(11)=0\)
balanced: \(f(00)=f(01)=0\) 和 \(f(10)=f(11)=1\)
让我们考虑解决问题的经典方法。从计算机科学的角度来看,我们经常对算法在最坏情况下的性能感兴趣;如果你尝试不到\(2^n\)的一半的组合,你仍然不能确定这个函数是constant还是balanced。因此,对于这个问题,经典的最坏情况需要我们尝试超过\(2^{n-1}\)种组合。
现在让我们考虑量子算法:
步骤1:
我们同样创建一个量子叠加: $\( H^{\otimes n}\left|0^{n}\right\rangle=\frac{1}{\sqrt{2^{n}}} \sum_{x \in\{0,1\}^{n}}|x\rangle \)$
步骤2:
我们应用同样的技巧将布尔函数的结果编码为符号,即, $\( \frac{1}{\sqrt{2^{n}}} \sum_{x \in\{0,1\}^{n}} U_{f}|x\rangle=\frac{1}{\sqrt{2^{n}}} \sum_{x \in\{0,1\}^{n}}(-1)^{f(x)}|x\rangle \)$ 如果它是constant,那么我们在第一步中就有原始状态。如果它是 balanced 的,那么我们的东西会更复杂,但我们可以让它变得简单。
步骤3:
回想一下 \(H|0\rangle=(|0\rangle+|1\rangle)/\sqrt{2}\) 和 \(H|1\rangle=(|0\rangle-|1\rangle)/\sqrt{2}\),其中减号只能在 \(|1\rangle\) 态前。 $\( \frac{1}{\sqrt{2^{n}}} \sum_{x \in\{0,1\}^{n}}(-1)^{f(x)} H^{\otimes n}|x\rangle=\frac{1}{2^{n}}\left(\sum_{x \in\{0,1\}^{n}}(-1)^{f(x)}\right)|000 \ldots 0\rangle+\ldots \)\( 此处未显示的部分在基向量中至少包含一个“1”。例如:\)H^{\otimes 2}|01\rangle=(|0\rangle+|1\rangle)(|0\rangle-|1\rangle) / 2=(1 / 2)|00\rangle+\ldots$
现在,我们可以很清楚地看到, constant 的幅度为 1,而 balanced 的幅度为 0。总之,我们可以通过应用一次oracle来解决问题,并检查最终输出是否在 \(|000\ldots 0\rangle\)。
from show_info import InfoTable
InfoTable('mindquantum', 'numpy')
| Software | Version |
|---|---|
| mindquantum | 0.11.0 |
| numpy | 1.26.4 |
| System | Info |
| Python | 3.11.10 |
| OS | Darwin arm64 |
| Memory | 17.18 GB |
| CPU Max Thread | 10 |
| Date | Tue Sep 16 18:01:39 2025 |