09. CC-U 门分解 & Toffoli 门

接下来的讨论是为之后证明CNOT与单比特门的集合的通用性做铺垫，我们需要一些分解线路的方法作为工具。

对于多控制门，我们考虑以下情况： $\( U=V^2 \)$ 存在以下等价线路：

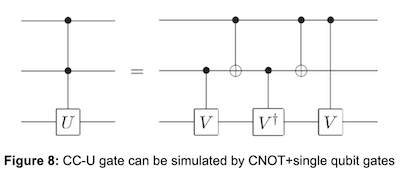
这是一种用受控V门简化CC-U门的标准分解方法。

为了理解它（不是证明它），让我们忘记第一个和最后一个控制操作。 在这种情况下，中间部分给出了以下变换：

\[\begin{split} \begin{aligned} |00\rangle & \rightarrow I \qquad \qquad |00\rangle\langle 00| \otimes I \rightarrow |00\rangle\langle 00| \otimes I \\ |11\rangle & \rightarrow I \qquad \qquad |11\rangle\langle 11| \otimes I \rightarrow |11\rangle\langle 11| \otimes V^2 \\ |01\rangle & \rightarrow V^\dagger \qquad \quad |01\rangle\langle 01| \otimes V^\dagger \rightarrow |01\rangle\langle 01| \otimes V^\dagger V \\ |10\rangle & \rightarrow V^\dagger \qquad \quad |10\rangle\langle 10| \otimes V^\dagger \rightarrow |10\rangle\langle 10| \otimes V V^\dagger \end{aligned} \end{split}\]

CC-U门的效果实际上是这样： $\( C_{U}=|00\rangle\langle 00|\otimes I+| 01\rangle\langle 01|\otimes I+| 10\rangle\langle 10|\otimes I+| 11\rangle\langle 11| \otimes U \)$ 如果我们现在应用回第一个和最后一个受控操作，那么我们会得到正确的答案。

我们也可以选择一个实例，用 MindQuantum 验证以上线路的等价性，现在我们令\(U = Y\)。

首先构建 CC-Y 门，可以通过list将多个控制位输入Y门的第二个参数得到多控制Y门。

from mindquantum.core.gates import Y
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += Y.on(2, [0, 1])
circ.svg()

接下来需要得到\(V\)使得\(V^2 = Y\)，这可以通过接口Power()实现。然后构建出相应线路。

from mindquantum.core.gates import Power, X

V = Power(Y, 0.5)
circ2 = Circuit()
circ2 += V.on(2, 1)
circ2 += X.on(1, 0)
circ2 += V.hermitian().on(2, 1)
circ2 += X.on(1, 0)
circ2 += V.on(2, 0)

circ2.svg()

将两个线路的矩阵进行比对，判断是否等价。

import numpy as np

is_equiv = np.allclose(circ.matrix(), circ2.matrix())
print(is_equiv)

True

可以看到，两个线路的对应矩阵完全相同。

Toffoli 门

当\(U = X\)时，得到的CC-X门被称为Toffoli门。在这种情况下，\(V=(1-i)(I+iX)/2\)。可以快速证明\(V\)是幺正的： $\( V^\dagger = (1+i)(I-iX)/2 \)\( 然后 \)\( V^{\dagger} V=\frac{1}{4}(1-i)(1+i)(I-i X)(I+i X)=\frac{1}{2}(I+I)=I \)\( 现在我们知道如何用CNOT+单比特门集合来模拟Toffoli门。接下来是Toffoli门的第一个应用，分解多控制\)U\(门： \)\( C_{n}(U)\left|x_{1} x_{2} x_{3} x_{4} x_{5}\right\rangle|\psi\rangle=\left|x_{1} x_{2} x_{3} x_{4} x_{5}\right\rangle U^{x_{1} x_{2} x_{3} x_{4} x_{5}}|\psi\rangle \)\( 下图中的\)|c_1\rangle,|c_2\rangle\cdots |c_5\rangle\(就等同于\)\left|x_{1} x_{2} x_{3} x_{4} x_{5}\right\rangle$：

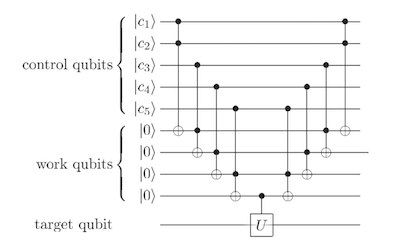
以上线路可以直接看出其效果：如果\(c_1\)和\(c_2\)都是\(|1\rangle\)，则第一个辅助比特翻转为\(|1\rangle\)；如果\(c_3\)和第一个辅助比特都是\(|1\rangle\)则第二个辅助比特翻转为\(|1\rangle\)（这意味着\(c_1,c_2,c_3\)都是\(|1\rangle\)），依此类推。因此最后只有所有控制位都为\(|1\rangle\)时才作用\(U\)门，即实现了多控制\(U\)门。

示例

考虑初态\(\alpha|00000\rangle|\psi\rangle+\beta|11111\rangle|\psi\rangle\)，插入中间的辅助量子比特后表示为\(\alpha|00000\rangle|0000\rangle|\psi\rangle+\beta|11111\rangle|0000\rangle|\psi\rangle\)。现在作用上述量子线路（到CU处截止），得到的量子态如下： $\( \alpha|00000\rangle|0000\rangle|\psi\rangle+\beta|11111\rangle|1111\rangle U|\psi\rangle \)\( 此时辅助比特与系统比特纠缠在一起，这不是我们想要的。因此我们需要在最后将它们全部重置为\)|0\rangle$态，这正是后半部分的那些顺序相反的Toffoli门的作用。

from show_info import InfoTable

InfoTable('mindquantum', 'numpy')

Software	Version
mindquantum	0.11.0
numpy	1.26.4
System	Info
Python	3.11.10
OS	Darwin arm64
Memory	17.18 GB
CPU Max Thread	10
Date	Tue Sep 16 18:00:55 2025

习题

Exercise 1

设上图中的多控制U门为\(U = R_x(\frac{\pi}{5})\)，请用MindQuantum验证多控制\(R_x\)门可以分解为多个Toffoli门和控制\(R_x\)门（验证线路矩阵等价）。