07. 两比特门

07. 两比特门#

CNOT门#

CNOT门应该是双比特门中最有名的一个，其作用在计算基矢的效果如下： $\( |00\rangle \rightarrow |00\rangle \)$

\[ |01\rangle \rightarrow |01\rangle \]
\[ |10\rangle \rightarrow |11\rangle \]
\[ |11\rangle \rightarrow |10\rangle \]

通常第一个比特被称为控制比特，第二个比特被称为目标比特。以上形式可以用更紧凑的形式表示： $\( |x,y\rangle \rightarrow |x,y\oplus x\rangle \)$

其中\(y\oplus x\)是按位乘法（模二加法），等同于异或门（XOR gate）。

以下是CNOT门的矩阵形式： $\( U_{\mathrm{CNOT}}=\left[\begin{array}{l} 1 \\ 0 \\ 0 \\ 0 \end{array}\right]\langle 00|+\left[\begin{array}{l} 0 \\ 1 \\ 0 \\ 0 \end{array}\right]\langle 01|+\left[\begin{array}{l} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]\langle 10|+\left[\begin{array}{l} 0 \\ 0 \\ 1 \\ 0 \end{array}\right]\langle 11|=\left[\begin{array}{llll} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{array}\right] \)$

在量子线路中，CNOT门用下面的符号表示：

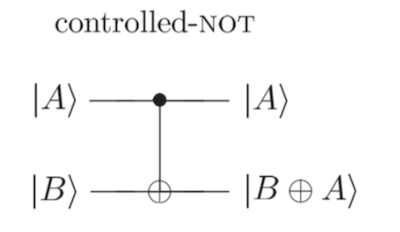
cnot in circuit

实际上CNOT门就是控制X门：

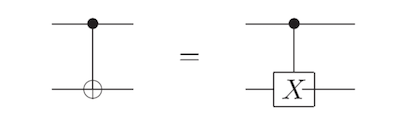
cnot equivalent

CNOT门是可逆的，并且有\(CNOT \enspace CNOT=I\)。

稍后我们将证明CNOT门与单比特门的集合对于量子计算是通用的，即我们可以用它们构造任意数量的量子比特的所有幺正变换。

在 MindQuanutum 中一般通过为X门添加控制位的方式得到CNOT门，因为 MindQuantum 可以简洁地为任意量子门添加控制位，只需要输入控制位作为第二个参数。也可以直接使用 CNOT 门（不推荐），CNOT(1, 0) 表示 q0 控制位 q1 目标位。

from mindquantum.core.gates import X, CNOT
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += X.on(1, 0)
circ += CNOT(1, 0)
print(circ)
circ.svg()

q0: ────■─────■─────
        ┃     ┃     
      ┏━┻━┓ ┏━┻━┓   
q1: ──┨╺╋╸┠─┨╺╋╸┠───
      ┗━━━┛ ┗━━━┛
_images/84390ee812edf4f8cac44392d1a833faf3a41c9cd3ed951fa13df70c18d2d931.svg

对于其它的量子门，同样可以用该方式添加控制位：

from mindquantum.core.gates import Y, RX
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += Y.on(1, 0)
circ += RX(1).on(2, 0)
circ.svg()
_images/e0cf1ab7f8abae585e4b5854358ab76266689e7d03800908625cee6db842b8ae.svg

如果需要更多控制位，只需要将 on 的第二个参数修改为列表即可：

from mindquantum.core.gates import X
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += X.on(0, [1, 2, 3])
circ.svg()
_images/920bd18863e5f1ef1ee28be853dba20a7a144b7e0f545929e4350d98d68c9de2.svg

SWAP门#

三个CNOT门可以构成SWAP门：

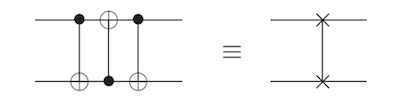
SWAP gate

作用于 0，1 基的效果如下： $\( \begin{aligned} |00\rangle & \rightarrow|00\rangle \rightarrow|00\rangle \rightarrow|00\rangle \\ |01\rangle & \rightarrow|01\rangle \rightarrow|11\rangle \rightarrow|10\rangle \\ |10\rangle & \rightarrow|11\rangle \rightarrow|01\rangle \rightarrow|01\rangle \\ |11\rangle & \rightarrow|10\rangle \rightarrow|10\rangle \rightarrow|11\rangle \end{aligned} \)$

可以看到，SWAP门的作用正是交换两个比特的量子态，数学表示如下：

\[ U_{S W A P}(\alpha|0\rangle+\beta|1\rangle)(\gamma|0\rangle+\delta|1\rangle)=(\gamma|0\rangle+\delta|1\rangle)(\alpha|0\rangle+\beta|1\rangle) \]

也可以记为以下形式：

\[ U_{S W A P}(\alpha \gamma|00\rangle+\beta \gamma|10\rangle+\alpha \delta|01\rangle+\beta \delta|11\rangle)=\alpha \gamma|00\rangle+\beta \gamma|01\rangle+\alpha \delta|10\rangle+\beta \delta|11\rangle \]

在MindQuantum中，SWAP门的用法与其它基本门相似，唯一的区别是它有两个目标比特，因此需要将包含两个目标位的list[int]作为参数输入：

from mindquantum.core.gates import SWAP
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += SWAP.on([1, 0])
print(circ)
circ.svg()

q0: ──╳───
      ┃   
      ┃   
q1: ──╳───
_images/cf563450f06ca3d3f733a22585bec51a784eb4564622ef1a02704499c2188538.svg 
from show_info import InfoTable

InfoTable('mindquantum')
Software Version
mindquantum0.11.0
System Info
Python3.11.10
OSDarwin arm64
Memory17.18 GB
CPU Max Thread10
DateTue Sep 16 18:00:22 2025

习题#

Exercise 1#

若\(q_0\)处于叠加态\(| \psi\rangle =\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\)，\(q_1\)处于\(|0\rangle\)态，现在对\(q_0\)、\(q_1\)作用CNOT门（控制位为\(q_0\)，目标位为\(q_1\)），请问该两比特系统的末态是什么样的，你是否能叫出它的名字？请用MindQuantum计算或验证你的结果。

Hint：Lecture 5 中我们学过，哈达玛门H作用在\(|0\rangle\)态效果如下： $\( H|0\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \)$

Exercise 2#

请你用MindQuantum验证SWAP门可以分解为三个CNOT门（即两者矩阵等价）。

目录