05. 旋转门

05. 旋转门#

首先我们需要给出以矩阵作为指数的自然指数函数的定义： $\(e^A \equiv I + A + \frac{1}{2!}A^2 + \frac{1}{3!}A^3 + \cdots\)$

引理： 如果 \(A^2 = I\)，那么有 $\(e^{i\theta A} = \cos\theta I + i\sin\theta A\)$

Proof：

\[\begin{split} \begin{align*} e^{i\theta A} & = I + i\theta A + \frac{1}{2!}(i\theta A)^2 + \frac{1}{3!}(i\theta A)^3 + \frac{1}{4!}(i\theta A)^4 + \cdots \\ & = I + i\theta A - \frac{1}{2!}\theta^2 I - \frac{1}{3!}i\theta^3 A + \frac{1}{4!}\theta^4 I + \cdots \\ & = \left( 1 - \frac{1}{2!}\theta^2 + \frac{1}{4!}\theta^4 - \cdots \right)I + \left(\theta - \frac{1}{3!}\theta^3 + \frac{1}{5!}\theta^5 - \cdots \right)iA \\ & = \cos\theta I + i\sin\theta A \end{align*} \end{split}\]

下面给出三个旋转门： $$

\[\begin{align*} R_x(\theta) & \equiv e^{-i{\theta\over 2} X} = \cos{\theta\over 2}I - i\sin{\theta\over 2} X\\ R_y(\theta) & \equiv e^{-i{\theta\over 2} Y} = \cos{\theta\over 2}I - i\sin{\theta\over 2} Y\\ R_z(\theta) & \equiv e^{-i{\theta\over 2} Z} = \cos{\theta\over 2}I - i\sin{\theta\over 2} Z\\ \end{align*}\]
\[ \begin{align}\begin{aligned}$R_x(\theta)$ 表示在Bloch球中，以 $x$ 轴为旋转轴，以右手法则确定旋转方向，旋转 $\theta$ 角度，$R_y$ 和 $R_z$ 同理。\\更一般的，如果以 $\vec{n}$ 为轴旋转 $\theta$ 角度，那么旋转算子为 $$R_{\vec{n}}(\theta) \equiv e^{-i(\theta / 2) n \cdot \sigma} = \cos{\theta\over 2}I - i\sin{\theta\over 2} \vec{n}\cdot \vec{\sigma}\end{aligned}\end{align} \]

其中 \(\vec{n} = (n_x, n_y, n_z) \in \mathbb{R}^3, n_x^2 + n_y^2 + n_z^2 = 1\)，\(\vec{\sigma} = (\sigma_1, \sigma_2, \sigma_3) = (X, Y, Z)\)。

该旋转算子可以生成任意的单量子比特旋转\(U\)（相差一个全局相位）。从某种意义上说，给定任何的\(U\)，人们总是可以选择角度\(\theta\)和旋转轴\(\hat{n}\)，使得 $\( U=e^{i\alpha}R_n(\theta) \)$

Lemma： \(\vec{n}\cdot \vec{\sigma}\) 的特征值是 \(\pm 1\).

Proof：

\[\begin{split} \begin{align*} \vec{n}\cdot \vec{\sigma} & = n_x X + n_y Y + n_z Z \\ & = \begin{pmatrix} 0 & n_x \\ n_x & 0 \\ \end{pmatrix} + \begin{pmatrix} 0 & -i n_y \\ i n_y & 0 \\ \end{pmatrix} + \begin{pmatrix} n_z & 0 \\ 0 & n_z \\ \end{pmatrix} \\ & = \begin{pmatrix} n_z & n_x-i n_y \\ n_x+ i n_y & -n_z \\ \end{pmatrix} \\ \\ \det\left(\vec{n}\cdot \vec{\sigma} - \lambda I\right) & = \begin{vmatrix} n_z - \lambda & n_x - i n_y \\ n_x + i n_y & -n_z - \lambda \end{vmatrix} \\ & = \lambda^2 - n_x^2 - n_y^2 - n_z^2 \\ & = \lambda^2 - 1 \end{align*} \end{split}\]

Theorem： \(R_{\vec{n}}(\theta)\) 的作用效果是在Bloch球中以 \(\vec{n}\) 为轴旋转 \(\theta\) 。

Proof：

因为 \(\vec{n} \cdot \vec{\sigma}\) 的特征值是 \(\pm 1\)，不妨设 \(+1\) 对应的特征向量是 \(|a\rangle\)，\(-1\) 对应的特征向量是 \(|b\rangle\)，那么根据谱分解定理，我们有 $\(\vec{n} \cdot \vec{\sigma} = \sum_i \lambda_i |i\rangle \langle i| = |a\rangle \langle a| - |b\rangle \langle b|\)$

对于任意单位向量 \(|\psi\rangle\)，将其用 \(\lbrace |a\rangle, |b\rangle\rbrace\) 这一组基表示，忽略全局相位 $$

\[\begin{align*} |\psi\rangle & = \alpha |a\rangle + \beta |b\rangle \\ & = \cos{\theta\over 2} |a\rangle + e^{i\phi} \sin{\theta\over 2} |b\rangle \end{align*}\]
\[考虑 $R_{\vec{n}}(\theta)$ 的作用效果： \]
\[\begin{align*} R_{\vec{n}}(\theta) & = \cos{\theta\over 2}I - i\sin{\theta\over 2} \vec{n}\cdot \vec{\sigma} \\ & = \cos{\theta\over 2}\left( |a\rangle \langle a| + |b\rangle \langle b| \right) - i\sin{\theta\over 2} \left( |a\rangle \langle a| - |b\rangle \langle b| \right) \\ & = \left( \cos{\theta\over 2} - i\sin{\theta\over 2} \right) |a\rangle \langle a| + \left( \cos{\theta\over 2} + i\sin{\theta\over 2} \right) |b\rangle \langle b| \\ & = e^{-i \frac{\theta}{2}} |a\rangle \langle a| + e^{i\frac{\theta}{2}} |b\rangle \langle b| \\ & = e^{-i \frac{\theta}{2}} \left( |a\rangle \langle a| + e^{i\theta}|b\rangle \langle b| \right) \end{align*}\]
\[因此作用后的向量 $|\psi'\rangle$ \]
\[\begin{align*} |\psi'\rangle & = R_{\vec{n}}(\alpha) |\psi\rangle \\ & = e^{-i \frac{\alpha}{2}} \left( \cos{\theta\over 2} |a\rangle \langle a| + e^{i(\phi + \alpha)} \sin{\theta\over 2} |b\rangle \langle b| \right) \end{align*}\]

$$

忽略掉全局相位，在Bloch球中，以 \(|a\rangle, |b\rangle\) 为轴，旋转 \(\alpha\) 角度。

下面我们来使用mindquantum来验证一下旋转效果。

首先我们构建一个线路来实现输入 \(\theta, \phi\) 输出对应的量子态，显然可以从 \(|0\rangle\) 通过两个旋转来实现。

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import RX, RZ, RY
import numpy as np

circ = Circuit()
circ += RY("theta").on(0)
circ += RZ("phi").on(0)
circ.svg()
_images/e131163536cc5716bf28d76c9b28794c79abd9d2f0788c34c80c069da991f4c8.svg

API 解释：

  • RX、RY、RZ 是常用的单比特旋转门，使用方法是 RX(name/val).on(q)，表示声名一个作用在 q 上的 \(R_x\) 门，如果参数是字符串 name 则生成一个含参量子门；如果参数是数值 val 则生成一个具体的量子门。在 MindQuantum 中只要两个参数名是相同的就表示同一个参数。

我们可以验证一下，\(\theta = \frac{\pi}{4}, \phi = 0\) 的点的坐标应该是 \((\frac{1}{\sqrt{2}}, 0, \frac{1}{\sqrt{2}})\)

from mindquantum.io.display import BlochScene
import matplotlib.pyplot as plt

%matplotlib widget

state1 = circ.get_qs(pr={"theta" : np.pi / 4, "phi" : 0})

scene = BlochScene()
fig, ax = scene.create_scene()
state1_obj = scene.add_state(ax, state1)
plt.show()

API 解释：

  • 对于含参量子线路，作用时需要传入具体的参数值。在 MindQuantum 中使用参数解析器 ParameterResolver，可以使用一个字典声名一个参数解析器，字典的结构是 {name: value} ；

  • 对于量子线路也可以调用 circ.get_qs()，表示将该线路作用在 \(|0\rangle\) 上的结果。

现在将它绕 \(z\) 轴旋转 \(\pi \over 3\)，旋转后的 \(\theta' = \frac{\pi}{4}, \phi' = \frac{\pi}{3}\)，旋转后的坐标为 \((\cos{\frac{\pi}{3}}\sin\frac{\pi}{4}, \sin\frac{\pi}{3}\sin\frac{\pi}{4}, \cos\frac{\pi}{4})\) 。

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import RX, RZ
from mindquantum.io.display import BlochScene
import numpy as np

%matplotlib widget

t = np.linspace(0, 1, num=100)  # 时间片
arr_theta = np.pi / 4 + 0 * t   # 每个时间点的 theta
arr_phi = np.pi / 3 * t         # 每个时间点的 phi
states = []                     # 存储每个时间点的 state
for theta, phi in zip(arr_theta, arr_phi):
    states.append(circ.get_qs(pr={"theta": theta, "phi": phi}))
states = np.array(states)

scene = BlochScene()
fig, ax = scene.create_scene()

# 先把 start 和 end 两个点画出来
start = circ.get_qs(pr={"theta": np.pi / 4, "phi": 0})
end = circ.get_qs(pr={"theta": np.pi / 4, "phi": np.pi / 3})
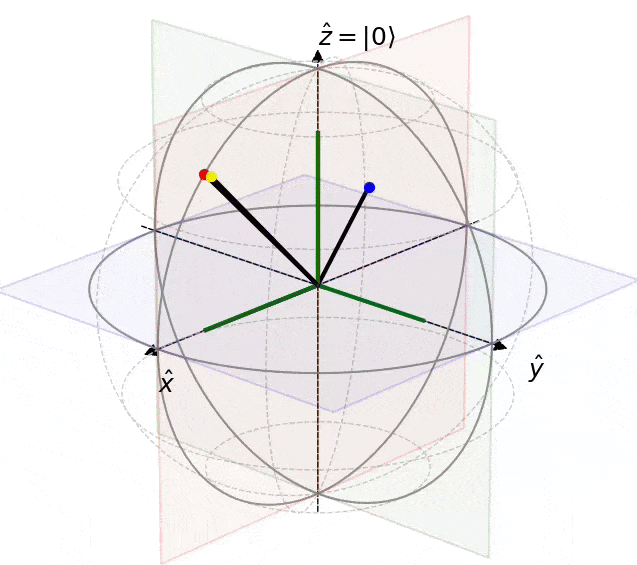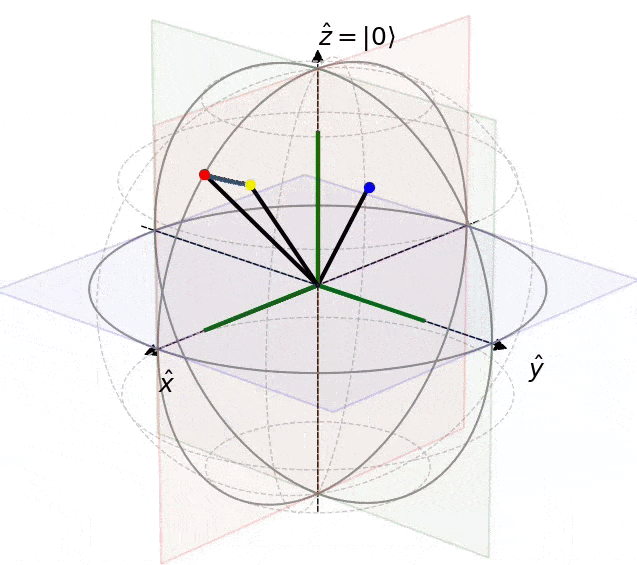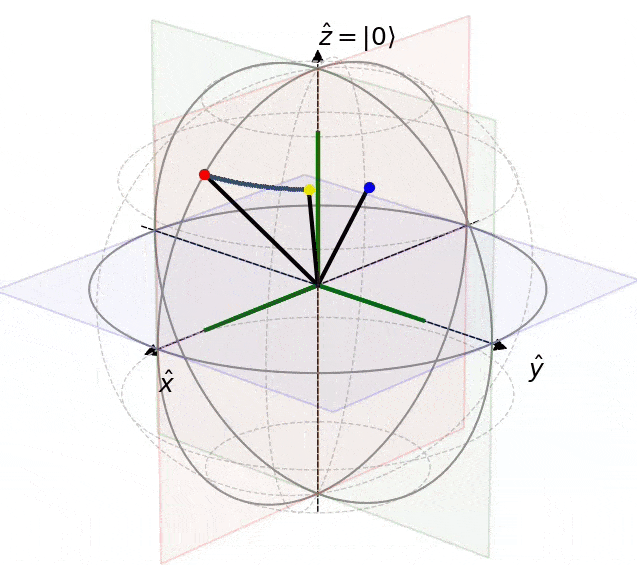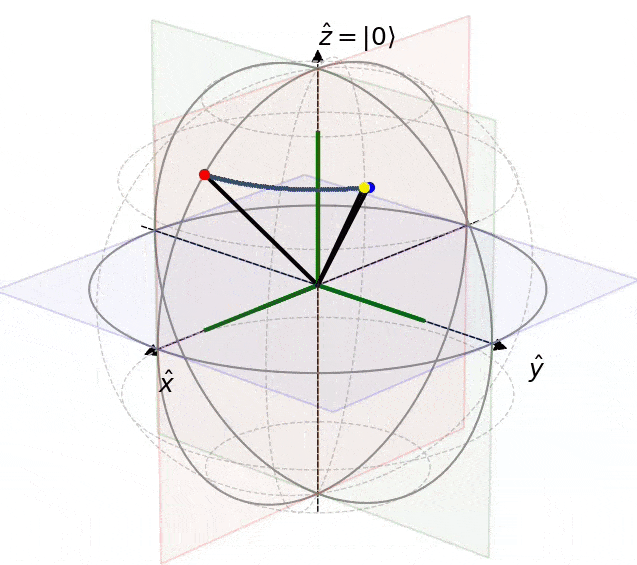
scene.add_state(ax, start, pointcolor="red")
scene.add_state(ax, end, pointcolor="blue")

# 生成动画
state_obj = scene.add_state(ax, states[0], pointcolor="yellow")
anim = scene.animation(fig, ax, state_obj, states)

/Users/jedzhou/miniconda3/envs/py311/lib/python3.11/site-packages/mindquantum/io/display/bloch_plt_drawer.py:533: UserWarning: jupyter environment detected, if animation not work, please install ipympl with '!pip install ipympl' in jupyter notebook and run '%matplotlib ipympl' in cell.
  warnings.warn(

rotate

API 解释：

  • scene.add_state 添加一个点；

  • scene.animation 生成动画，需要把每个时间点的 state 数组传入。

Bloch 球的颜色等许多参数都可以调节，详细 API 参照 mindquantum.io 。

旋转门的性质（以\(R_z\)门为例）#

\(R_z\)门有以下几个特性： $\( X R_{z}(\theta) X=R_{z}(-\theta)=R_{z}(\theta)^{-1}=R_{z}(\theta)^{\dagger} \)\( 最后的关系式来源于\)R_z(\theta)\(的幺正性。验证一下，\)(Z^\dagger=Z)\( \)\( R_{z}(\theta)^{\dagger}=I \cos \frac{\theta}{2}+i Z \sin \frac{\theta}{2}=e^{i \theta Z / 2} \)$ 第一个关系式也是正确的，有如下两种方式验证：

  1. 直接的办法，已知\(R_{z}(\theta)(\alpha|0\rangle+\beta|1\rangle)=\alpha e^{-i \theta / 2}|0\rangle+\beta e^{i \theta / 2}|1\rangle\)，则有 $\( \begin{aligned} X R_{z}(\theta) X(\alpha|0\rangle+\beta|1\rangle) &=X R_{z}(\theta)(\alpha|1\rangle+\beta|0\rangle) \\ &=X\left(\alpha e^{i \theta / 2}|1\rangle+\beta e^{-i \theta / 2}|0\rangle\right) \\ &=\alpha e^{i \theta / 2}|0\rangle+\beta e^{-i \theta / 2}|1\rangle \end{aligned} \)\( 然后与\)R_{z}(-\theta)(\alpha|0\rangle+\beta|1\rangle)=\alpha e^{i \theta / 2}|0\rangle+\beta e^{-i \theta / 2}|1\rangle$比较。

  2. “更好”的方法可能是： $\( X R_{z}(\theta) X=X I X \cos \frac{\theta}{2}-i X Z X \sin \frac{\theta}{2}=I \cos \frac{\theta}{2}+i Z \sin \frac{\theta}{2} \)\( 因为我们知道\)X Z X=-Z \(，或 \) Z X+X Z=0 \( 亦或 \) X Z=-X Z$（对于任何泡利矩阵的组合都成立）

Figure from wikipedia

commutative_relation

  • 注意到\(XY-YX=2iZ\)，这意味着\(XY=iZ\)。两个不同的泡利矩阵相乘与第三个泡利矩阵成正比。

  • 现在让我们在 MindQuantum 中验证上述性质，我们随便选取一个\(\theta\)的值，然后观察\(X R_{z}(\theta) X\)、\(R_{z}(-\theta)\)、\(R_{z}(\theta)^{-1}\)和\(R_{z}(\theta)^{\dagger}\)作用在\(|0\rangle\)态上的结果是否相同。

from mindquantum.core.gates import RZ, X
from mindquantum.core.circuit import Circuit

theta = 1

# X Rz(𝜃) X
circ = Circuit()
circ += X.on(0)
circ += RZ(theta).on(0)
circ += X.on(0)
print(circ)
print(circ.get_qs(ket=True))

      ┏━━━┓ ┏━━━━━━━┓ ┏━━━┓   
q0: ──┨╺╋╸┠─┨ RZ(1) ┠─┨╺╋╸┠───
      ┗━━━┛ ┗━━━━━━━┛ ┗━━━┛   
(0.87758256+0.47942554j)¦0⟩

# Rz(-𝜃)
circ2 = Circuit()
circ2 += RZ(-theta).on(0)
print(circ2)
print(circ2.get_qs(ket=True))

      ┏━━━━━━━━┓   
q0: ──┨ RZ(-1) ┠───
      ┗━━━━━━━━┛   
(0.87758256+0.47942554j)¦0⟩

# inverse of Rz(𝜃)
from mindquantum.core.gates import Power
circ3 = Circuit()
circ3 += Power(RZ(theta), -1).on(0)
print(circ3)
print(circ3.get_qs(ket=True))

      ┏━━━━━━━━━━┓   
q0: ──┨ RZ(1)^-1 ┠───
      ┗━━━━━━━━━━┛   
(0.87758256+0.47942554j)¦0⟩

# Rz(𝜃) with dagger
circ4 = Circuit()
circ4 += RZ(theta).hermitian().on(0)
print(circ4)
print(circ4.get_qs(ket=True))

      ┏━━━━━━━━┓   
q0: ──┨ RZ(-1) ┠───
      ┗━━━━━━━━┛   
(0.87758256+0.47942554j)¦0⟩

可以看到四种方式得到的线路末态完全一致。

from show_info import InfoTable

InfoTable('mindquantum')
Software Version
mindquantum0.11.0
System Info
Python3.11.10
OSDarwin arm64
Memory17.18 GB
CPU Max Thread10
DateTue Sep 16 18:00:03 2025

习题#

Exercise 1#

写出 \(R_x(\theta), R_y(\theta), R_z(\theta)\) 的矩阵形式。

Exercise 2#

证明 \(XR_y(\theta)X = R_y(-\theta)\)

Exercise 3（选做）#

证明如下等式成立： $\( e^{-i(\theta / 2) n \cdot \sigma}=c_{\theta} I-i s_{\theta}(n \cdot \sigma) \)\( 其中\)n\cdot\sigma\equiv n_x X+n_y Y+n_z Z\(，且\)n_x^2+n_y^2+n_z^2=1$。

Exercise 4（选做）#

证明：给定任意的\(U\)，人们总是可以选择角度\(\theta\)和旋转轴\(\hat{n}\)，使得 $\( U=e^{i\alpha}R_n(\theta) \)$

目录