16. Solovay-Kitaev 算法

16. Solovay-Kitaev 算法#

Solovay-Kitaev 算法#

现在，我们已经了解到，使用 THTH 序列之类的东西，我们可以将任何单个量子比特门逼近到任何精度，但是性能似乎很差。Solovay-Kitaev 算法旨在加快逼近门的过程。SK 算法的适用性比我们先前所讨论的要广泛，因此，我们需要学习\(\epsilon\)-net 的概念。什么是\(\epsilon\)-net \(V_\epsilon\)？我们已经见过一个（在上一节的最后一个等式中）。简单来说，给定一个任意的酉门，如果我们有一个 \(\epsilon\)-net，那么我们应该能够用某个门\(V\in V_\epsilon\)来近似\(U\)，精度为\(\epsilon\)，即

\[ \boxed{ \|U-V\| \equiv \operatorname{tr} \sqrt{(U-V)^{\dagger}(U-V)} \leq \epsilon } \]

上式等价于\(\left\|U V^{+}-I\right\| \leq \epsilon\)。

此外，逆应当存在，即如果我们有\(V\)， 则我们有\(V^\dagger\)。

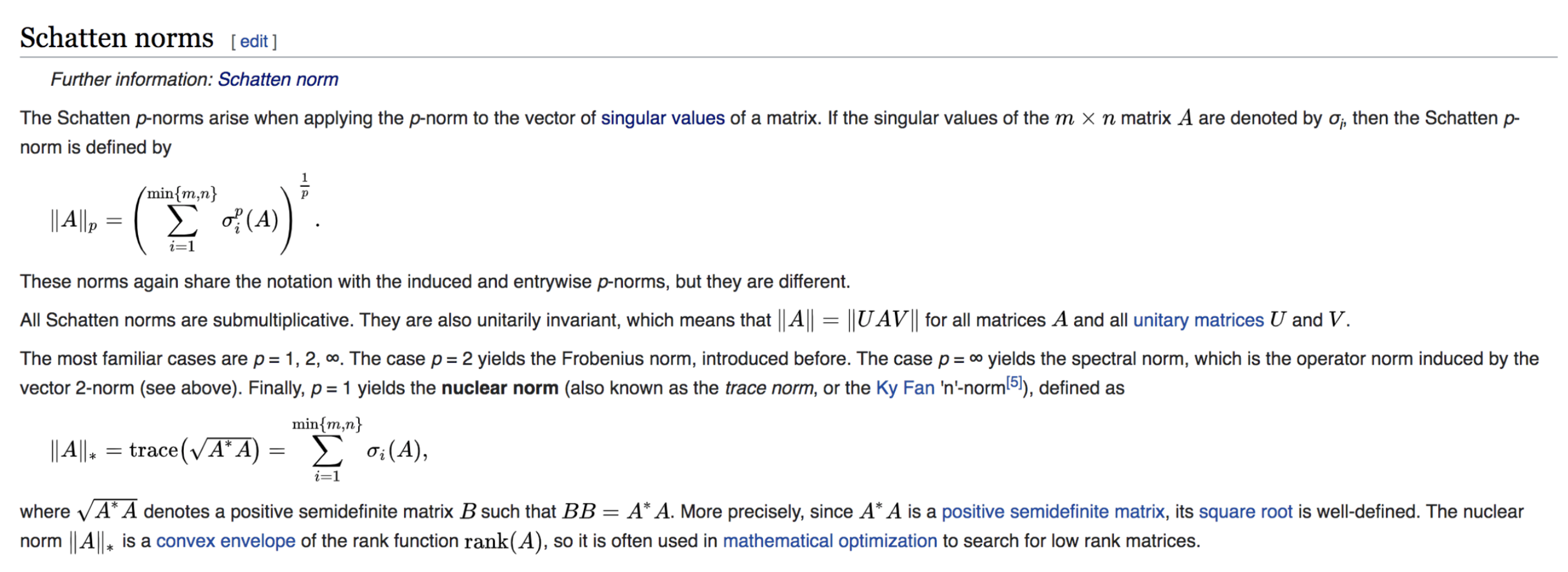
让我们仔细研究对于一个任意矩阵的（迹）范数：\(\|A\|=\operatorname{tr}\sqrt{A^\dagger A}\)

  • 若\(A\)是厄米的，即\(A^\dagger=A\)，那么\(\|A\|=\left|a_{1}\right|+\left|a_{2}\right|+\left|a_{3}\right|+\ldots\)是特征值的绝对值之和。

  • 对于任何幺正矩阵\(U\)，\(\|U A\|=\operatorname{tr}\sqrt{A^\dagger U^\dagger U A}=\|A\|\)。

也可以参考

Schatten norms

我们要做的是从 \(\epsilon\)-net 构造一个更精确的近似值 \(\epsilon^{3/2}=\epsilon \cdot \epsilon^{1/2}<\epsilon\)。

\[ \boxed{ \left\|U V^{\dagger}-W\right\|=\|U-W V\|=O\left(\epsilon^{3 / 2}\right) } \]

其中\(W\)是 epsilon 网络中门的乘积。这是一个令人惊讶的结果，通常我们认为近似值应该是\(O\left(\epsilon\right)\)。

  • 如果每一步都花费\(O\left(\epsilon\right)\)，n 步将是\(O\left(n \epsilon\right)\)

  • 请记住，这里的错误是系统性的，这意味着它无法被消除。

证明

  • 首先，让我们定义（你总是可以这样做）

    \[ U V^\dagger \equiv e^{iA} \]

其中我们有 \(\|A\| = O(\epsilon)\)，且\(\|e^{iA}-I\|=\|iA\|=O(\epsilon)\)。等价的，我们可以只写\(A=O(\epsilon)\)。

  • 接下来，我们要找到一个记为\(W\)的门的乘积，以最小化范数：\(\|U V^\dagger - W\|=\|e^{iA} - W\|\)。为了继续，我们需要知道一个有趣的关系：对于任何给定的\(A\)，总是可以找到一对（它们可能不是唯一的）矩阵\(B\)和\(C\)使得

    \[ [B, C]=-iA \]

其中\(\|B\|=\|C\|=O(\epsilon^{1/2})\)。

  • 对于量子比特，你可以想象我们可以旋转参考系，因此\(A = O(\epsilon)Z\)。那么，自然地，我们可以选择\(B=O(\epsilon^{1/2}X)\)和\(C = O(\epsilon^{1/2})Y\)。

备注：虽然\(A\)有点小，但它的数学表达式是准确已知的。因此，\(B\)和\(C\)也是已知的。

  • 现在，让我们尝试以下方法：

    \[ \boxed{ W \equiv e^{i B^{\prime}} e^{i C^{\prime}} e^{-i B^{\prime}} e^{-i C^{\prime}}=I-\left[B^{\prime}, C^{\prime}\right]+O\left(\epsilon^{3 / 2}\right) } \]

其中门\(e^{iB'}\)是\(e^{iB}\)的近似值，并且类似地\(e^{iC'}\)是\(e^{iC}\)的近似值。这意味着\(\left\|e^{i B^{\prime}}-e^{i B}\right\|=O(\epsilon),\left\|e^{i C^{\prime}}-e^{i C}\right\|=O(\epsilon)\)，进而得到\(\|B'-B\|=O(\epsilon)\)和\(\|C'-C\|=O(\epsilon)\)。

  • 让我们进行验证：

    \[ e^{i B^{\prime}} e^{i C^{\prime}} e^{-i B^{\prime}} e^{-i C^{\prime}}=\left(I+i B^{\prime}+O(\epsilon)\right)\left(I+i C^{\prime}+O(\epsilon)\right)\left(I-i B^{\prime}+O(\epsilon)\right)\left(I-i C^{\prime}+O(\epsilon)\right) \]

如果你只查看一阶项，它们会被相互抵消。为什么二阶项只包含\([B', C']\)？(homework)

  • 现在，如果我们关注对易子，我们有

    \[ \left[B^{\prime}, C^{\prime}\right]=[B+O(\epsilon), C+O(\epsilon)]=[B, C]+O\left(\epsilon^{3 / 2}\right) \]

这意味着你可以将\([B', C']\)替换为\([B, C]= -iA\)。换句话说，

\[ W=I+i A+O\left(\epsilon^{3 / 2}\right)=e^{i A}+O\left(\epsilon^{3 / 2}\right) \]

这完成了证明。

因此，我们现在从\(\epsilon\)-net有效地构建了一个\(\epsilon^{3/2}\)-net，代价是总共应用5个门，即\(WV=e^{i B^{\prime}} e^{i C^{\prime}} e^{-i B^{\prime}} e^{-i C^{\prime}}V\)，这来自于\(\epsilon\)-net。现在，如果我们再次替换整个论点，那么我们会得到一个更好的网络（如果我们不关心额外的门）：\(~(\epsilon^{3/2})^{3/2}=\epsilon^{(3/2)^2}\)。更严格地，让我们通过（上限）量化新误差

\[ \epsilon_{1}=c \epsilon_{0}^{3 / 2} \quad \text { or } \quad c^{2} \epsilon_{1}=\left(c^{2} \epsilon_{0}\right)^{3 / 2} \]

其中\(\epsilon_0\)是 epsilon-net 中的原始值，并且\(c\)是某个常数。

此外，如果需要花费（最大）\(L_0\)基本门在\(\epsilon\)-net 中实现\(V\)，那么需要花费\(L_1=5L_0\)个门\(\{e^{i B^{\prime}}, e^{i C^{\prime}}, e^{-i B^{\prime}}, e^{-i C^{\prime}}, V\}\)来构建\(\epsilon^{3/2}\)-net。如果我们更进一步，那么我们有

\[ \epsilon_{2}=c \epsilon_{1}^{3 / 2} \quad \text { or } \quad c^{2} \epsilon_{2}=\left(c^{2} \epsilon_{1}\right)^{3 / 2}=\left(c^{2} \epsilon_{0}\right)^{(3 / 2)^{2}} \]

下一次（第 2 级），你需要应用来自 \(\epsilon^{3/2}\)-net 的集合来近似门集合如\(\{e^{i B^{\prime}}, e^{i C^{\prime}}, e^{-i B^{\prime}}, e^{-i C^{\prime}}, WV \}\) 。那将是\(5(5L_0)\)个门。

一般来说，在级别 \(k\)，我们有

\[ c^{2} \epsilon_{k}=\left(c^{2} \epsilon_{k-1}\right)^{3 / 2}=\left(c^{2} \epsilon_{0}\right)^{(3 / 2)^{k}} \]

我们总共需要\(L_k=5L_{k-1}=5^k L_0\)。

现在，我们的情况是，如果我们愿意支付应用指数个门（以 \(k\) 为单位）的成本，那么我们会在缩小误差方面获得双指数效应。因此，我们可能会获得一些优势（homework）

\[ \frac{L_{k}}{L_{0}}=5^{k}=\left(\frac{\log \left(1 / c^{2} \epsilon_{k}\right)}{\log \left(1 / c^{2} \epsilon_{0}\right)}\right)^{\log 5 / \log (3 / 2)} \]

如果我们忘记了常量，那么我们有更标准的形式：

\[ L_{k}=O\left(\log \left(1 / \epsilon_{k}\right)^{3.97}\right) \]

这个表达式告诉我们，如果我们想要实现\(\epsilon_k\)大小的近似值，那么您预计每个门都会有\(O\left(\log \left(1 / \epsilon_{k}\right)^{3.97}\right)\)的额外成本，这只会带来多项式开销。例如，在某个\(n\)量子比特的量子算法中，我们有一个 poly(n) 的电路。 将每个门改进为 \(\epsilon_k\)后，我们仍然有一个多项式电路。