08. 控制门

下面介绍一个例子——控制Z门（CZ门）：

from mindquantum.core.gates import Z
from mindquantum.core.circuit import Circuit

circ = Circuit()
circ += Z.on(1, 0)
circ.svg()

这个门的作用是：

1. 当控制比特q0为1时，对目标比特q1作用Z门；

2. 当控制比特q0为0时，不做任何操作；

也就是说： $$

\[\begin{align*} |00\rangle & \rightarrow |00\rangle \\ |01\rangle & \rightarrow |01\rangle \\ |10\rangle & \rightarrow |10\rangle \\ |11\rangle & \rightarrow -|11\rangle \end{align*}\]

\[写成矩阵形式： \]

\mathcal{U}_{CZ} = \begin{bmatrix} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & -1 \end{bmatrix} $$

CZ门具有一个性质，交换控制比特和目标比特后，作用效果不变。

from mindquantum.core.gates import Z
from mindquantum.core.circuit import Circuit
from IPython.display import display_svg
import numpy as np

circ1 = Circuit()
circ1 += Z.on(1, 0)
display_svg(circ1.svg())

circ2 = Circuit()
circ2 += Z.on(0, 1)
display_svg(circ2.svg())

print(np.allclose(circ1.matrix(), circ2.matrix()))

True

我们可以使用 CZ 门和 Hadamard 门来实现 CNOT 门。

from mindquantum.core.gates import Z, H, CNOT
from mindquantum.core.circuit import Circuit
from IPython.display import display_svg
import numpy as np

circ1 = Circuit()
circ1 += H.on(0)
circ1 += Z.on(1, 0)
circ1 += H.on(0)
display_svg(circ1.svg())

circ2 = Circuit()
circ2 += CNOT.on(0, 1)
display_svg(circ2.svg())

print(np.allclose(circ1.matrix(), circ2.matrix()))

True

控制U门

CZ门是一种特殊的 \(C(U)\) 门，其中 \(U = Z\)。一般来说，\(C(U)\) 门的定义为：

1. 控制比特为1时，对目标比特作用 \(U\) 门；

2. 控制比特为0时，不作用（作用 \(I\) 门）；

相位

考虑一种简单情形 \(U = e^{i\alpha}I\)。

如果仅仅是单量子比特，那么 \(e^{i\alpha}\) 作为全局相位，我们可以忽略它（全局相位在物理上没有观测效应）。

如果是 \(C(U)\) 二量子比特门，此时就不能忽略掉 \(e^{i\alpha}\)。不妨设 \(|q_1 q_0\rangle\)，控制比特是 q0： $$

\[\begin{align*} |00\rangle & \rightarrow |00\rangle \\ |01\rangle & \rightarrow e^{i\alpha}|01\rangle \\ |10\rangle & \rightarrow |10\rangle \\ |11\rangle & \rightarrow e^{i\alpha}|11\rangle \end{align*}\]

\[对于一般的 $|\psi\rangle = a |00\rangle + b |01\rangle + c|10\rangle + d|11\rangle$，作用效果为： \]

\[\begin{align*} |\psi'\rangle & = a |00\rangle + be^{i\alpha}|01\rangle + c|10\rangle + de^{i\alpha}|11\rangle \\ & = \left[I \otimes \left(|0\rangle \langle 0| + e^{i\alpha} |1\rangle \langle 1|\right) \right] |\psi\rangle \end{align*}\]

$$

因此 \(C(e^{i\alpha}I)\) 等价于一个单量子比特门。

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import UnivMathGate, I
from IPython.display import display_svg
import numpy as np
from numpy.random import rand

alpha = rand()
print(f"alpha = {alpha}")

u = UnivMathGate("U", np.array(
    [[np.exp(complex(0, alpha)), 0], 
     [0, np.exp(complex(0, alpha))]]))
circ1 = Circuit()
circ1 += u.on(1, 0)
display_svg(circ1.svg())

p = UnivMathGate("U'", np.array(
    [[1, 0],
     [0, np.exp(complex(0, alpha))]]
))
circ2 = Circuit()
circ2 += p.on(0)
circ2 += I.on(1)
display_svg(circ2.svg())

print(np.allclose(circ1.matrix(), circ2.matrix()))

alpha = 0.9496466347941014

True

API 解释：

• UnivMathGate(name, mat) 通过矩阵 mat 声名一个名为 name 的量子门。

实现 C(U)

根据 lecture7 我们知道 \(U = e^{i\alpha}AXBXC\)，其中 \(ABC = I\)。这意味着我们可以用如下的电路实现 \(C(U)\) ：

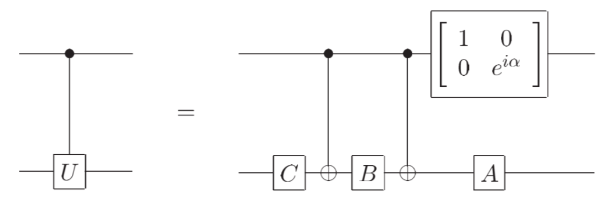
下面我们证明这件事情：

不妨设 控制比特 \(q_0 = a|0\rangle + b|1\rangle\)，目标比特 \(q_1 = |t\rangle\) 。

左边的线路作用的结果为： $\(C_U |\psi\rangle = a|0\rangle |t\rangle + b|1\rangle U|t\rangle\)$

右边的线路一步步的作用结果： $$

\[\begin{align*} |\psi\rangle & = a|0\rangle |t\rangle + b|1\rangle |t\rangle \\ & \rightarrow a|0\rangle C|t\rangle + b|1\rangle C|t\rangle \\ & \rightarrow a|0\rangle C|t\rangle + b|1\rangle XC|t\rangle \\ & \rightarrow a|0\rangle BC|t\rangle + b|1\rangle BXC|t\rangle \\ & \rightarrow a|0\rangle BC|t\rangle + b|1\rangle XBXC|t\rangle \\ & \rightarrow a|0\rangle ABC|t\rangle + e^{i\alpha}b|1\rangle AXBXC|t\rangle \\ & = a|0\rangle |t\rangle + b|1\rangle U|t\rangle \end{align*}\]

$$

下面对 \(C(H)\) 门进行验证。

因为 \(H = e^{i\pi\over 2}R_z(0)R_y({\pi\over 2})R_z(\pi)\)，所以令 $\( \begin{cases} A = R_z(\beta)R_y({\gamma\over 2}) \\ B = R_y(-{\gamma\over 2})R_z(-{(\delta+\beta)\over 2}) \\ C = R_z({(\delta-\beta)\over 2}) \end{cases} \)$

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import RZ, RY, RZ, X, H, CNOT
from mindquantum.core.gates import PhaseShift
from IPython.display import display_svg
import numpy as np
from numpy.random import rand

alpha = np.pi / 2
beta = 0
gamma = np.pi / 2
delta = np.pi

circ1 = Circuit()
circ1 += H.on(1, 0)
display_svg(circ1.svg())

# A = RZ(beta) * RY(gamma / 2)
# B = RY(-gamma / 2) * RZ(-(delta + beta) / 2)
# C = RZ((delta - beta) / 2)
circ2 = Circuit()
circ2 += RZ((delta-beta)/2).on(1)
circ2 += CNOT.on(1, 0)
circ2 += RZ(-(delta + beta)/2).on(1)
circ2 += RY(-gamma / 2).on(1)
circ2 += CNOT.on(1, 0)
circ2 += RY(gamma / 2).on(1)
circ2 += RZ(beta).on(1)
circ2 += PhaseShift(alpha).on(0)
display_svg(circ2.svg())

print(np.allclose(circ1.matrix(), circ2.matrix()))

True

拓展的控制门

下面介绍一些常用的记号，用来拓展控制门的功能。

我们使用“实心圆”表示控制比特为“1”时作用，使用“空心圆”表示控制比特为“0”时作用：

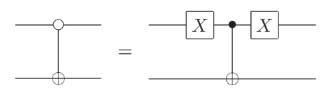
两个线路是等价的，因为 $$

\[\begin{align*} & |0\rangle \langle 0| \otimes X + |1\rangle \langle 1| \otimes I \\ = & X |1\rangle \langle 1|X \otimes X + X|0\rangle \langle 0|X\otimes I \\ = & \left(X\otimes I \right) \left(|0\rangle \langle 0| \otimes X + |1\rangle \langle 1|\otimes I\right) \left(X\otimes I\right) \end{align*}\]

$$

使用 MindQuantum 验证：

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import X, CNOT, UnivMathGate
import numpy as np

U = UnivMathGate("U", np.array(
    [[0, 0, 1, 0],
     [0, 1, 0, 0],
     [1, 0, 0, 0],
     [0, 0, 0, 1]]
))
circ1 = Circuit()
circ1 += U.on([0, 1])

circ2 = Circuit()
circ2 += X.on(0)
circ2 += CNOT.on(1, 0)
circ2 += X.on(0)
print(np.allclose(circ1.matrix(), circ2.matrix()))
circ2.svg()

True

我们也可以有多个目标比特，等价于多个单目标比特的作用。

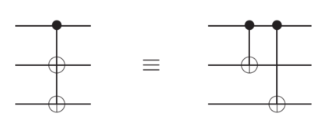
多控制比特

如果控制比特数目为 \(n\) 个，记作 \(C^n(U)\)，作用效果如下： $\(C^n(U) |x_1x_2\ldots x_n\rangle |t\rangle = |x_1x_2 \ldots x_n\rangle U^{x_1x_2\cdots x_n}|t\rangle\)\( 当且仅当 \)x_1 = x_2 = \cdots = x_n = 1\( 时，对目标比特作用 \)U$ 操作。

from mindquantum.core.circuit import Circuit
from mindquantum.core.gates import X

circ = Circuit([X.on(0, [1, 2])])
print(circ.matrix())
circ.svg()

[[1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.+0.j 0.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.+0.j 0.+0.j 0.+0.j]
 [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.+0.j]
 [0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 0.+0.j 1.+0.j 0.+0.j]]

from show_info import InfoTable

InfoTable('mindquantum', 'numpy')

Software	Version
mindquantum	0.11.0
numpy	1.26.4
System	Info
Python	3.11.10
OS	Darwin arm64
Memory	17.18 GB
CPU Max Thread	10
Date	Tue Sep 16 18:00:48 2025

习题

Exercise 1

使用 H 门来实现 交换 CNOT 门的控制比特和目标比特。

Exercise 2

使用 CNOT 和 单量子比特门 来构造 \(R_y(\theta)\) 。